Earth's Rotation Day 2025 is on Wednesday, January 8, 2025: Day Length-Earth's Rotation?

Wednesday, January 8, 2025 is Earth's Rotation Day 2025. The First Earth Day was March 21 ... the earth rotates a full

Ever feel like you're simply spinning around and around? Do not worry-- most of us are, constantly! Planet's Rotation Day is a little reminder that we're all turning uncontrollable, and there's absolutely nothing that we could do regarding it.

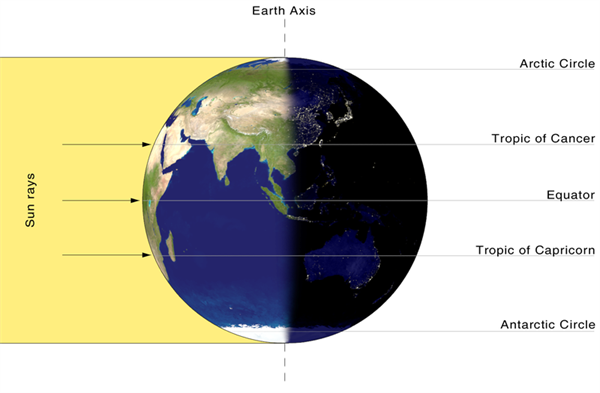
Acceleration g usually referred to as gravitational acceleration actually has two components, gravitational and centrifugal. On equator:

g = gg - gc

where

gg is "real" gravitational acceleration because of attraction caused by Earth's mass

gc centrifugal component because of Earth's rotation

gg = GM / R^2

M - mass of the Earth M = 5.974x10^24 kg

G - gravitational constant G = 6.674x10^-11 m^3/kg/s^2

R - equatorial radius of the Earth, R = 6378.1 km

gc = w^2 R

w - angular velocity of rotation

w = 2 pi / T

where

T - period of rotation, T= 24h = 86400s

I interpret your question as how large should gc be so that

g = gg - gc = 0

or

gg = gc

I'm not going to use Earth's mass in calculation. Instead, I'll obtain gg from ge:

ge = gg - gco

ge - measured equatorial surface gravity g = 9.78m/s^2

gco - current centrifugal acceleration on equator.

gco = wo^2 R

gg = ge + wo^2 R = w^2 R = gc

ge + (2 pi / To)^2 R = (2 pi / T)^2 R

T = 2 pi To sqrt [R / (ge To^2 + 4 pi^2 R)]

T = 5065s = 1h 24min 25s

Of course, we could neglect gco to get

ge = 4 pi^2 R / T^2

T = sqrt [4 pi^2 R / ge]

T = sqrt [4 pi^2 6378.1x10^3 / 9.78] = 5074 s

T = 1h 24min 34s

Neglect gco (centrifugal contribution to measured gravitational acceleration on the equator) means to assume that acceleration ge=9.78m/s^2 is exclusive result of the Earth's gravity.

How does earth's orbit and rotation effect the length of a year and the change from day to night?

Earth's rotation period relative to the Sun (true noon to true noon) is its true solar day or apparent solar day. It depends on the Earth's orbital motion and is thus affected by changes in the eccentricity and inclination of Earth's orbit. Both vary over thousands of years[1] so the annual variation of the true solar day also varies. Generally, it is longer than the mean solar day during two periods of the year and shorter during another two.[n 1] The true solar day tends to be longer near perihelion when the Sun apparently moves along the ecliptic through a greater angle than usual, taking about 10 seconds longer to do so. Conversely, it is about 10 seconds shorter near aphelion. It is about 20 seconds longer near a solstice when the projection of the Sun's apparent movement along the ecliptic onto the celestial equator causes the Sun to move through a greater angle than usual. Conversely, near an equinox the projection onto the equator is shorter by about 20 seconds. Currently, the perihelion and solstice effects combine to lengthen the true solar day near December 22 by 30 mean solar seconds, but the solstice effect is partially cancelled by the aphelion effect near June 19 when it is only 13 seconds longer. The effects of the equinoxes shorten it near March 26 and September 16 by 18 seconds and 21 seconds, respectively.[2][3][4]

The average of the true solar day during the course of an entire year is the mean solar day, which contains 86,400 mean solar seconds. Currently, each of these seconds is slightly longer than an SI second because Earth's mean solar day is now slightly longer than it was during the 19th century due to tidal friction. The average length of the mean solar day since the introduction of the leap second in 1972 has been about 0 to 2 ms longer than 86,400 SI seconds.[5][6][7] Random fluctuations due to core-mantle coupling have an amplitude of about 5 ms.[8][9] The mean solar second between 1750 and 1892 was chosen in 1895 by Simon Newcomb as the independent unit of time in his Tables of the Sun. These tables were used to calculate the world's ephemerides between 1900 and 1983, so this second became known as the ephemeris second. In 1967 the SI second was made equal to the ephemeris second.[10]

The apparent solar time is a measure of the Earth's rotation and the difference between it and the mean solar time is known as the equation of time.

Earth's rotation period relative to the fixed stars, called its stellar day by the International Earth Rotation and Reference Systems Service (IERS), is 86,164.098 903 691 seconds of mean solar time (UT1) (23h 56m 4.098 903 691s, 0.997 269 663 237 16 mean solar days).[11][n 2] Earth's rotation period relative to the precessing or moving mean vernal equinox, misnamed its sidereal day,[n 3] is 86,164.090 530 832 88 seconds of mean solar time (UT1) (23h 56m 4.090 530 832 88s, 0.997 269 566 329 08 mean solar days).[11] Thus the sidereal day is shorter than the stellar day by about 8.4 ms.[13] In 499 CE Aryabhata, a great mathematician-astronomer from the classical age of Indian mathematics and Indian astronomy estimated the length of sidereal day as 23h 56m 4.1s.[14]

Both the stellar day and the sidereal day are shorter than the mean solar day by about 3 minutes 56 seconds. The mean solar day in SI seconds is available from the IERS for the periods 1623–2005[15] and 1962–2005.[16]

See more...

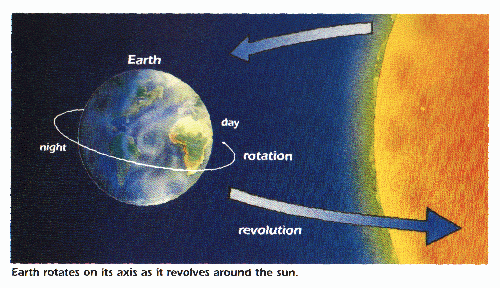
Confusion about the sidereal day and the Earth's rotation?

I think a better definition is that a sidereal day is the time it takes the Earth to rotate a full circle, or 360 degrees around. What they mean by "relative to the stars" is that after 1 sidereal rotation, the stars are in the same position in the sky as they previously were. That is, lets say Vega is directly overhead. As the Earth rotates, the star will move and set. After a full sidereal rotation, the star Vega will again be in the same position directly over head. (Of course stars also slightly move over the course of the year but it will be relatively in the same position).

This contrasts the solar day. The solar day is referenced from the sun. In this measurement, a day is defined as the time from one point on the earth facing the sun, until that point faces it again. This is actually more than a 360 degree turn. The reason is because the Earth moves slightly along its orbit. In doing so, the Earth must rotate slightly more to again face the sun. Check out this orrery for a good visible display.